Updated Trinity Study for 2024 – More Withdrawal Rates!
| Updated: |(Disclosure: Some of the links below may be affiliate links)
Would you like to know precisely which withdrawal rate is safe and will sustain your lifestyle for a long time?
You will find the answer in this article with updated results from the Trinity Study! This study researched different withdrawal rates for retirement. Although the original research was not about early retirement, it is often referred to in the Financial Independence and Retire Early (FIRE) movement!
However, there are two caveats to the original study. First, they are only covering the period until 1995. And then, they are not covering more than thirty years of retirement. Thirty years is not enough for some people wanting to retire early.
Therefore, I reproduce the original study’s results with recent data all the way to 2023! And I extended the data back to 1871. This makes for much more data than the original study.
I have also considered periods as long as 50 years. It means many more withdrawal simulations than the original study.
In this article, you will find how I did it and all the results I have gathered from this data!
The Trinity Study
I have already talked at great length about the Trinity Study. It is an excellent research paper done by three professors from Trinity University.
Their research paper’s goal was to see which withdrawal rates people should use to sustain a particular lifestyle for up to 30 years. It is important to note that the original research was not about early retirement but official retirement.
It is important to emphasize that we are talking about sustaining a lifestyle (expenses), not capital. So, if you end up with 1 USD at the end of the retirement period, this is a success. If you want to sustain your capital in retirement, it is a different success criterion not treated by the original Trinity study.
They tested the success rates of withdrawal rates from 3% to 12%. Also, they tested portfolios with between 0% and 100% stocks by jumps of 25%.
The authors also took inflation into account in the results. Indeed, it is interesting to compare the results with and without inflation. Finally, they also provided the terminal values of the portfolio.
I wrote a detailed article about the Trinity Study if you want more information.
The 4% Rule (of Thumb)
The Trinity Study is the source of the 4% Rule. This rule states that if you only withdraw 4% of your initial portfolio yearly, you can sustain your lifestyle for a very long period. And your withdrawal is adjusted for inflation every year.
Some people believe that the original study shows that this will sustain forever. But this is not what the original research was about. They only tested simulations for up to 30 years.
It is better to call it The 4% Rule of Thumb. Because if you plan to retire very early, you will probably need a lower withdrawal rate. Moreover, your withdrawal rate will depend on your portfolio and asset allocation to stocks and bonds.
Why did I do it again?
If the study is excellent, why did I want to redo it? I have several reasons for that.
First, I wanted to see how this worked with recent stock market returns. The original study was only covering years up to 1995. I wanted to have more recent data. I wanted to ensure the results were holding with more recent stock market behavior. So this simulation will cover returns until the end of 2023!
Secondly, the original study only covered up to thirty years of retirement. I wanted to ensure that the portfolio could sustain withdrawals for extended periods. For people retiring early, I think that 50 years is not unreasonable.
Finally, I have to admit that I like to write code. So it was cool to write code related to this blog. And being a big geek, now I can run many simulations with the data I want. Overall, it was a lot of fun preparing the data for this article.
Ultimately, I want to extend the Trinity Study to the European markets. It will be challenging to obtain the data. But I will try to find it for as many years as possible.
How I redid the Trinity Study
My simulation uses monthly withdrawals. Most people in retirement will withdraw money monthly. It is also possible to withdraw money at the end of the year instead. But I believe that it is not common.
I have calculated all the returns monthly. Doing that makes the results much more accurate than doing it yearly. And the monthly withdrawal is updated with inflation every month as well. Every possible starting month in the available data is tested.
For this simulation, I have not done any rebalancing. For more information, I have compared different rebalancing methodologies for retirement.
Withdrawals are based on the current allocation. For instance, if your base allocation to stocks is 60%, but your current allocation is 80%, 80% of the withdrawal will be taken from stocks. I may use different withdrawal techniques in the future.
Based on this simulation, I collected the same results as the original study: success rates without inflation, success rates with inflation, and terminal values.
Success Rates of the Trinity Study
I start the simulation with the entire data from 1871 to 2023.
In this simulation, success is when your portfolio does not run out of money before the end of the simulation. For instance, if we simulate for 20 years and end up with one dollar after 20 years, it is a success. This is a failure if the portfolio runs out of money before that (it could be in the first year or the nineteenth year).
So, the success rate is the percentage of the months that end up with success. The higher the success rate, the better the results are.
We will see what success rates we have when we ignore inflation. We start with 20 years since I do not think anybody will care about a ten-year-long simulation. I will begin at a 3% withdrawal rate and go up to 12%, increasing by 1% at a time.
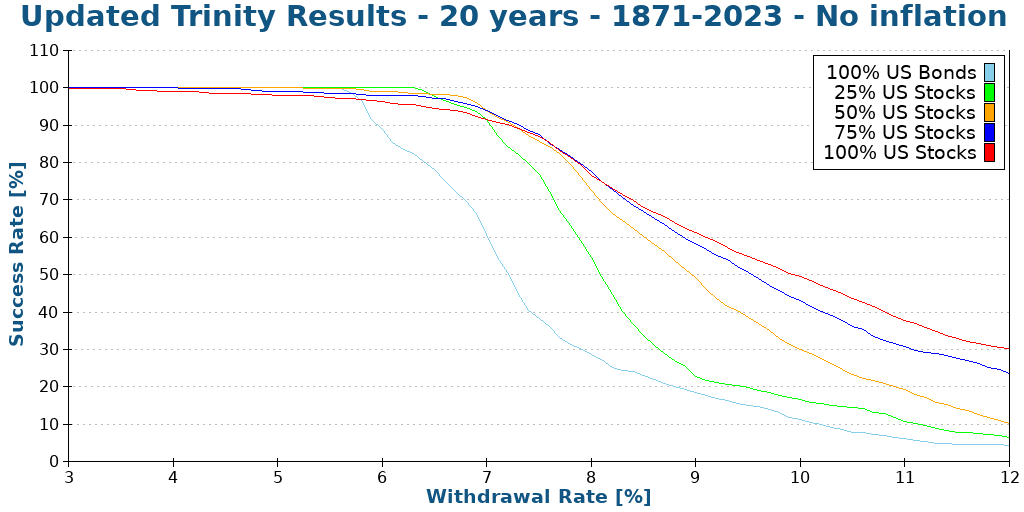
We can see what we already expect:
- Increasing the withdrawal rate decreases the chances of success
- Any withdrawal rate higher than 8% does not make sense long-term, even without inflation.
- A small allocation of bonds can help with lower withdrawal rates
- Generally, a 100% stock portfolio will perform better than the other portfolios.
Here is what happens when we push the simulation to 30 years.
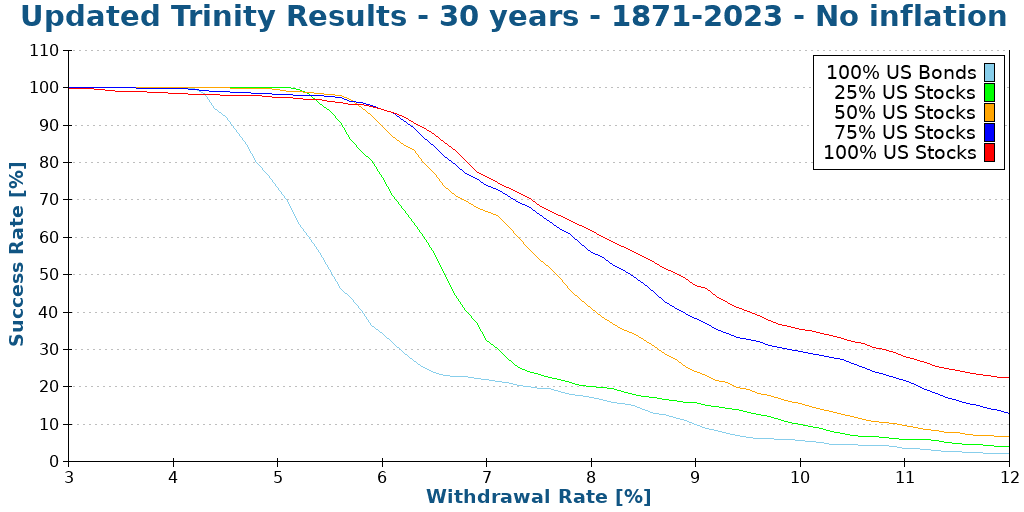
We can see that increasing the number of years decreases the likelihood of success. It is logical since you are more likely to run out of money.
With 30 years of retirement without inflation, a 6% withdrawal rate with a significant allocation to stocks still makes a lot of sense!
Taking Inflation into Account for retirement
However, it is much better to consider inflation in our simulation! We see again with 20 years to compare the results:
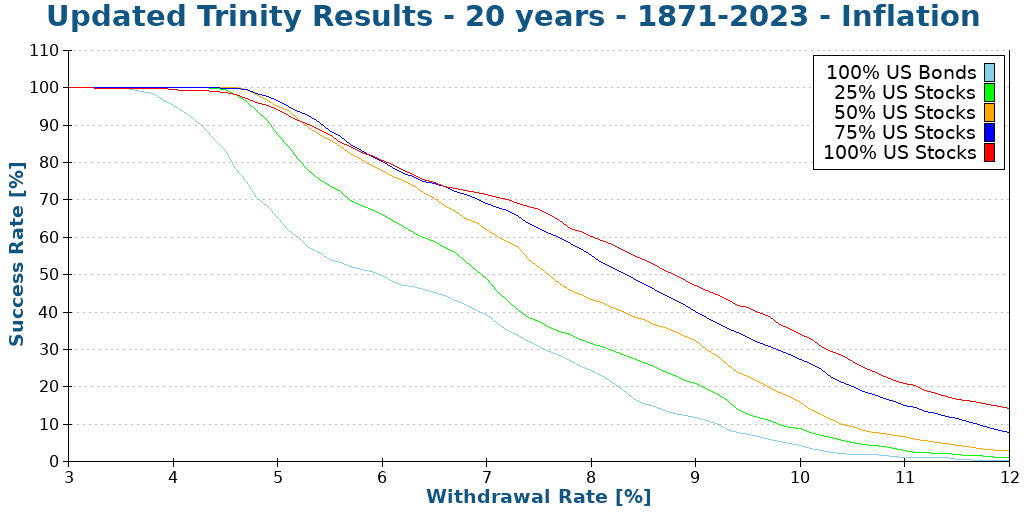
As we can see, inflation causes a significant hit to our chances of success! Before inflation, an 8% withdrawal rate made some sense. Now 6% is the limit. And even 6% has a barely over 75% chance of success!
Here is what happens in 30 years.
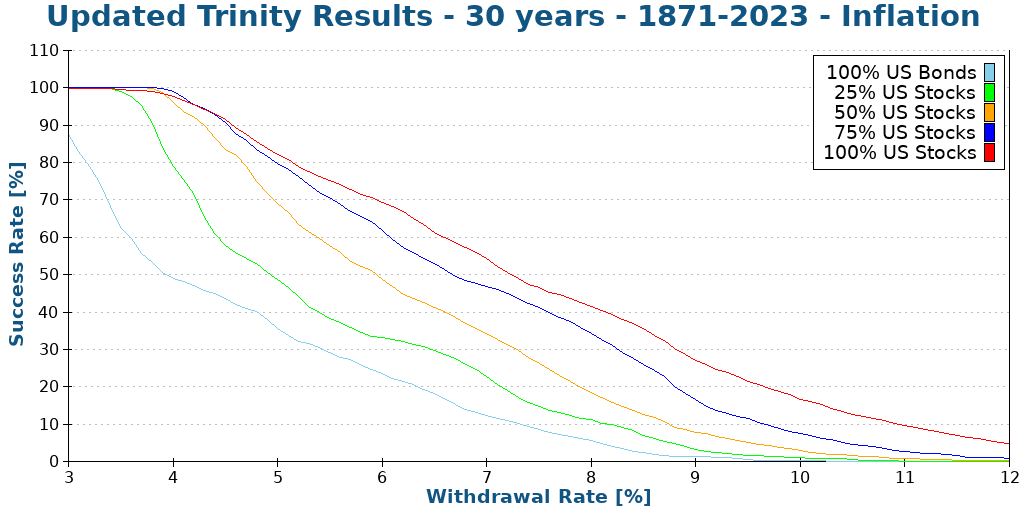
We can now see that anything higher than a 6% withdrawal rate is hazardous, with a less than 75% chance to succeed even with 100% stocks.
More withdrawal rates
Since we see that reasonable withdrawal rates are in the range of 3% to 6%, we try more withdrawal rates. I have simulated increments of 0.1% of withdrawal rates.
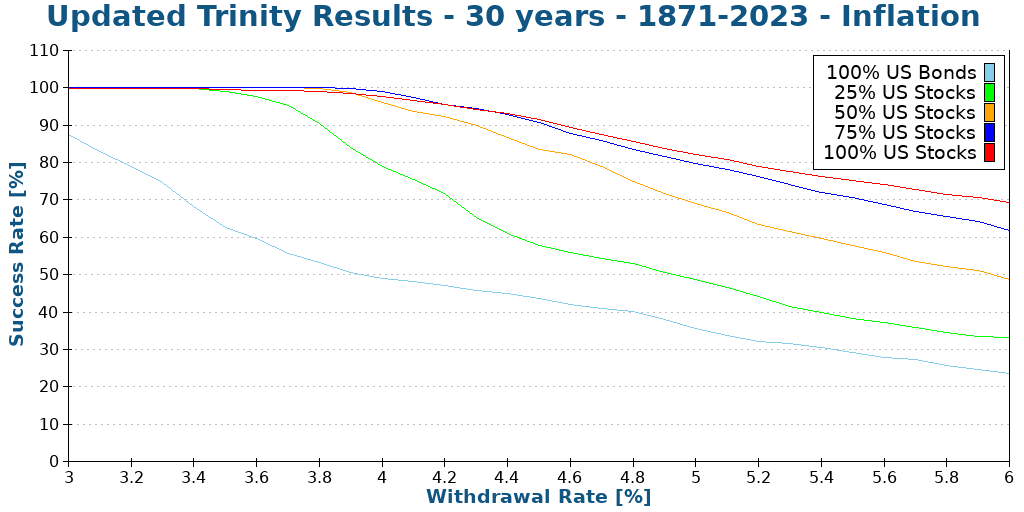
With a large stock allocation, withdrawal rates between 3% and 4% are very safe. Some people would even dare use withdrawal rates of about 4.5%. But even a portfolio with 100% stocks has only an 85% chance of success after 30 years with 4.5%.
Longer retirement time
One of the caveats of the original study is that they stopped at 30 years. We run the same simulation again but with 40 years this time.
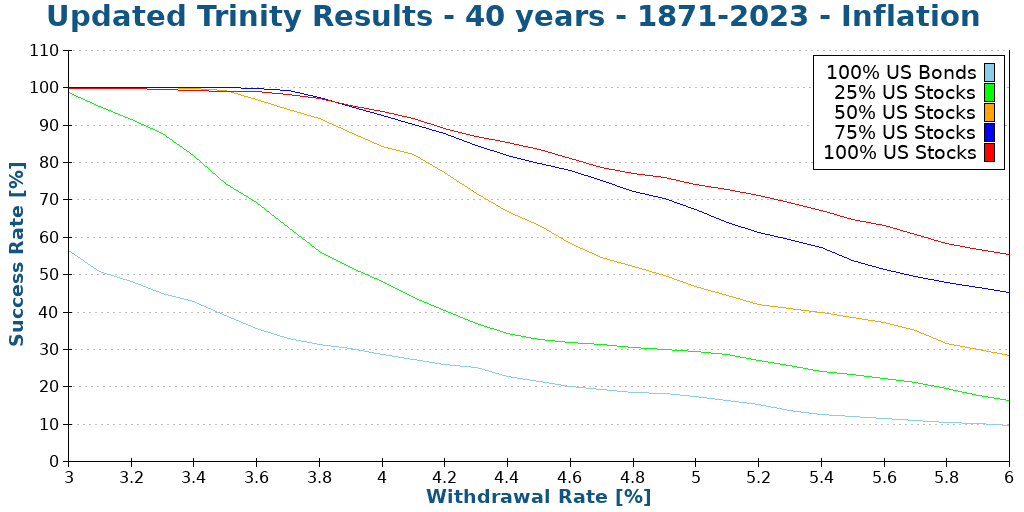
After 40 years, we are starting to see lower success rates, even for most people’s 4% withdrawal rate. Unless you have 100% of stocks, your success rate will be less than 90%.
Here is what happens with 50 years.
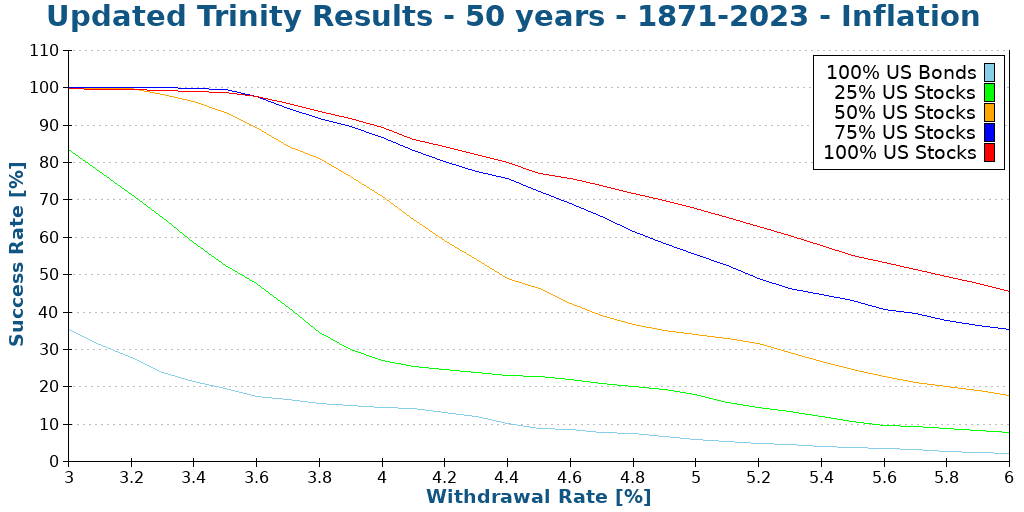
As expected, we see lower success rates. But it is still not bad at all with reasonable withdrawal rates. A 100% allocation to stocks and a 3.5% withdrawal rate still have more than a 98% success rate. This is significantly more than I expected.
It shows that the study’s original conclusion can still hold for over 30 years. It is excellent news!
Updated Terminal Values
Another interesting thing from the study was that they also compared the terminal values of the different withdrawal rates and portfolios.
So we will see the terminal values of a 1000$ portfolio after 30 years. I did the simulation for a portfolio of 100% Stocks. For the sake of display, I have reduced the number of withdrawal rates.
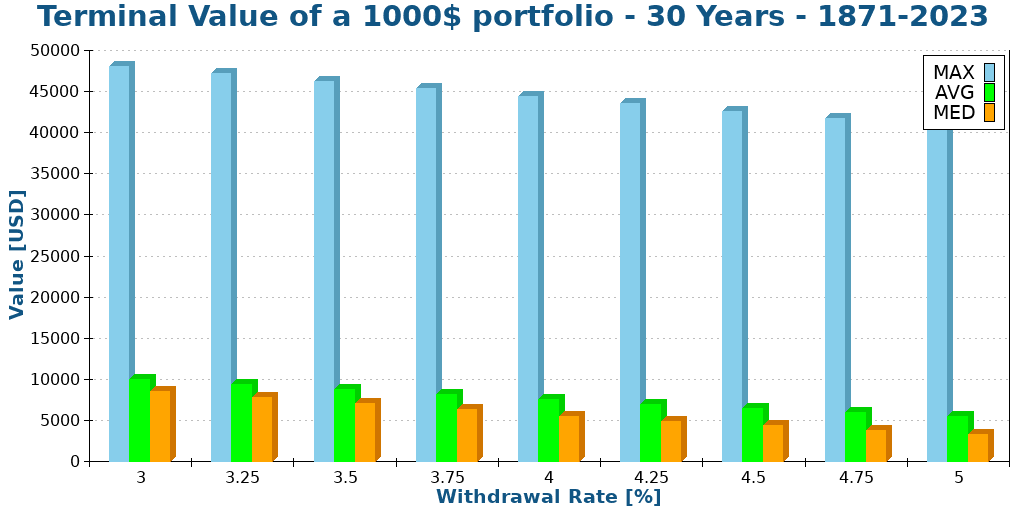
I did not show the minimum values. Indeed, they are always zero. If the chance of failure exceeds zero, the minimum value will be zero.
However, the average and median values are quite remarkable. We will focus on the median since it is generally more representative than the average.
For a withdrawal rate of 3.5%, my current target, the median terminal value after 30 years, is about 6700 dollars! Not only did your portfolio sustain your lifestyle, but it also increased six-fold! Let me repeat this. After 30 years of doing nothing but withdrawing money, you have six times more money than when you started!
The maximum values do not mean a lot. But it is crazy to see that after 30 years, you could have about 30 times more money than when you started! And this is with a 3.5% withdrawal rate!
Here is what happens when we extend it to 40 years.
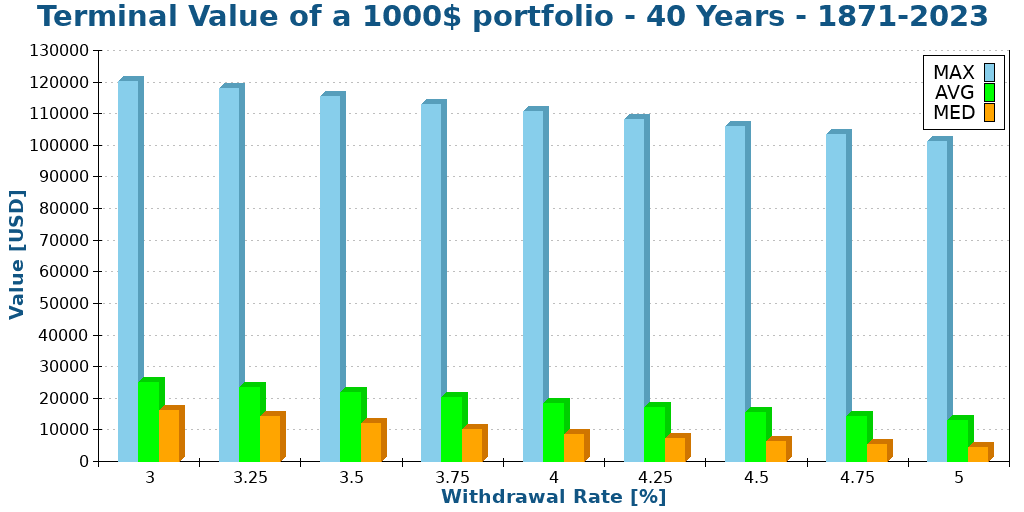
We can see that the results are comparable. However, all the values are significantly higher. The numbers are all about twice higher. On average, your retirement money will double during the ten additional years. So, even though you are not contributing more money and living from it, your portfolio will double in 10 years. How cool does that sound?
The success rate is not everything
There is something important with these measurements: the success rate does not tell the entire story. For instance, for you, which of these two scenarios is better:
- 98% to last 50 years, but a chance of running out after ten years
- 96% to last 50 years, but a chance of running out after 48 years
For me, the second scenario is better. You do not want to have a chance of failing after only ten years if you are planning for 50 years. But if it fails after 48 years, you have many years to make some adaptations.
So, another quite important metric is the worst duration of a scenario. This means after how many months, the first failure can happen.
For reference, here are the success rates of each portfolio for 50 years and different withdrawal rates:

And now, here are the worst durations for each of these portfolios:
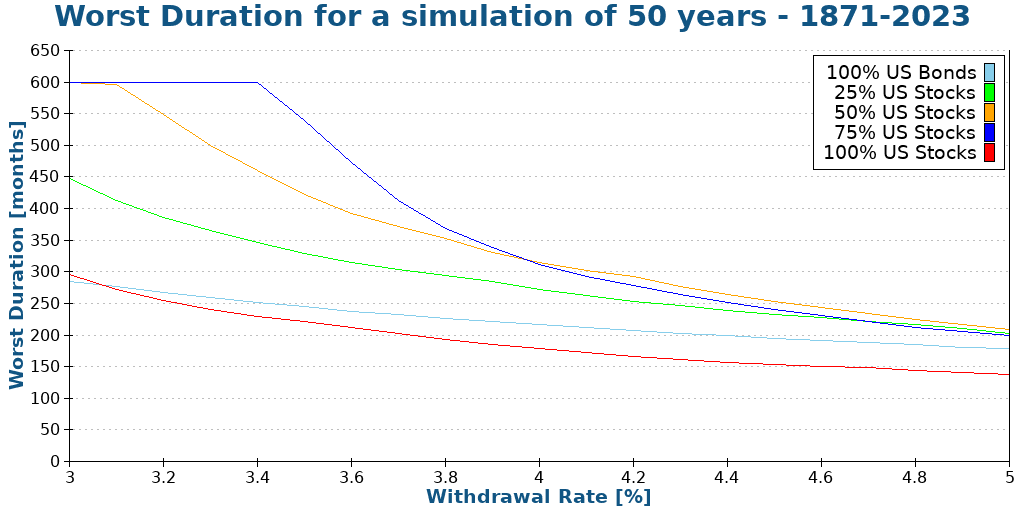
If we only look at the first graph, the conclusion is that higher allocation to stocks is always better. But if we look at the second graph, 100% stocks is the worst one!
So what does this mean: you need a balance in your portfolio. Bonds will significantly reduce the chances of your portfolio failing too early. This does not mean that you should optimize for the highest worst duration either. Because if your highest duration is 40 years, but you have only a 50% chance of reaching 50 years, this is gambling, not planning.
So balance is essential. While stocks will increase your success, stocks are more subject to sequences of return risks.
How to implement the Trinity Study?
Now that we have seen that the results of the Trinity Study are encouraging and would let people retire early, how should we implement it?
Theoretically, the Trinity Study is based on a simple concept: you can retire based on a large principal by withdrawing with a fixed withdrawal rate.
However, in practice, this means you need to accumulate money, more than most people accumulate during their lifetime. And you need to accumulate this earlier than retirement age.
To accumulate this money is not easy, but it is also not complicated. First, you need to save money (as much as possible). For this, you will need to focus on your expenses and earnings.
Then, you will need to invest that money until you can retire. Once you have accumulated the proper amount through capital gains and savings, you will be financially free.
If you are interested, I have many articles on my blog about financial independence.
How did I do it?
You can find my code and my data on Github. Everything is available to share as much as possible!
I wrote the entire program in C++. I used this programming language because it is my favorite! And it is blazing fast! I have not especially optimized my code, and it takes less than a second to generate thousands of simulations.
If you are not a coder, I also have an online FIRE calculator to do most of the calculations presented here.
My U.S. and international data is based on the data made available by Big ERN in its Safe Withdrawal Rate series. It is a good dataset that has been tested several times already. Big ERN made all this available for free. I am very thankful for his work! I have completed its data with the missing years using the same methodology.
If you want to use the graphs in this article, please cite this article as the source of the image!
Future of the series
It was fascinating to reproduce these results. And it was very insightful as well. I have learned many things from the results. It is great to see the confirmation that the original conclusions hold for more than 50 years.
And it also shows that my withdrawal rate (3.5%) is a safe bet. I may switch to 3.75% in the future. I will have to run more simulations. It is important to choose a proper safe withdrawal rate.
Talking of simulations, I have run a few more simulations with the same idea:
- Trinity Study Results with Swiss Stocks
- Withdrawal rates and low-yield bonds
- When should you rebalance your portfolio?
- Does the Trinity Study work in recent years?
- How often should you withdraw money?
Since I plan to make more articles like these with more simulations, I would like to get your point of view on this article! Please let me know what you think in the comments below! What should I improve?
What do you think of these results? Would you like me to run more simulations like this? Do you have ideas on what kind of simulations I should run next?
Conclusions
With all these results, we can have several important conclusions.
First, the paper’s original conclusions still hold even with much more data being considered. And it still stands accurate up to 2024! It is excellent since it shows that the 4% rule of thumb still works!
If you increase the simulation time to more than 30 years, a 4% withdrawal rate is no longer safe. With 50 years of retirement, you have a 90% chance of success with a 4% withdrawal rate at most. A withdrawal rate of around 3.5% would be safer for most people.
If you want real chances of success, you will need more than 50% of your portfolio allocated to stocks. The stocks allow us to fight inflation and cover the withdrawal rate year after year.
If you choose a reasonable withdrawal rate, you will likely have much more money than when you started! For instance, a 3.5% withdrawal rate over 30 years with 100% stocks would leave you about six times more money than when you started!
For information about the original study, read my detailed article about the Trinity Study. If you are extremely conservative, you will also be interested in learning how to choose a failsafe withdrawal rate.
If you want to start investing to become Financially Independent, you will be interested in my guide on how to get started in the stock market.
Download this e-book and optimize your finances and save money by using the best financial services available in Switzerland!
Download The FREE e-book
Great research. Thank you very much. I mean i also can invest 380000 Euro into the S&P 500. Than thanking out 4 percent every year would not be a problem. When the market crashes or is in a bear market phase i have some savings in my cash account which i can use. So the drawdown is not realy a problem.
Keep in mind that you are taking 4% of the initial sum, not of the current sum. Depending on how many years you have in front of you, 4% may be safe, but for very long term, it may not be. And dont’ forget about the exchange rates.
Indeed, using a cash cushion can help.