What is Compound Interest? Is it Magic?
| Updated: |(Disclosure: Some of the links below may be affiliate links)
Compound interest is a subject you can read about on most personal finance blogs. I have already talked a little bit about it. But I never delved into it. It is now time to cover compound interest in detail.
Many people will tell you that compound interest is like magic! However, it is only math. But how can we calculate compound interest? Even if it is not magic, its effects are more powerful than it seems at first sight. The compounding results make investing in the stock market so appealing. But does the stock market compound? We will try to answer these questions in this article.
I think many people do not correctly understand that compound interest. This article will help you understand compound interest and why it is excellent.
Compound Interest
We will start with a quote attributed to Albert Einstein:
Compound interest is the greatest mathematical discovery of all time
There is some controversy as to whether he said that. People attribute him several quotes about compounding interest, such as saying it is the eighth wonder of the world or even saying it is the most potent force in the universe. Over the years, many quotes have been wrongly attributed to Einstein. I would not be surprised if he did not say anything like that.
Regardless of who said what, compound interest is a powerful instrument.
Compound interest is straightforward to understand. Compound interest is interest over interest. Standard interest gives interest only to the principal. However, with compound interest, the principal includes all the previous interest you received. That means that you get interest over an increasingly large principal. It may not sound like a big difference, but it is significant. Compound interest will always return more than standard interest.
But this is not magic. Compound Interest is simple math, as seen in the next section. And almost everything compounds these days. Even though the results are great, I would hardly call that magic.
Calculating the future value
Now, we will have to do some math. Since interest is computed over the accumulated principal and not only the basic principal, it is a bit more complicated to calculate the future value of your money than with standard interest, where it is trivial.
First of all, it is necessary to know the interest (I) and the principal (P), of course. But you also need to know the compounding period. That is the frequency of compounding or when the interest is calculated. For most banks, compounding is done daily. To compute compound interest for the stock market, you must consider the average yearly returns as interest and an annual period.
Once you have all these values, you can compute the Future Value (FV) of your money after n compounding periods with this formula:
FV = P ( 1 + I ) ^ n
This formula will only work if the interest (I) is in the same time unit as n. Generally, you have a yearly interest rate (r) and some compounding periods per year (t):
FV = P ( 1 + r/n ) ^ nt
These formulas will give you the value of your money in the future.
Of course, you do not have to do the math yourself if you do not want to. Indeed, there are many calculators out there on the internet that will do the job just fine for you. For instance, the calculator on investor.gov is quite good. It is operated by the U.S. Securities and Exchange Commission (SEC), which is interestingly regulating the stock market. The calculator from financial-calculators.com is also quite easy to use and has more options. And there are hundreds of other calculators on the internet if you are unsatisfied with these two.
A few examples
We can see the result with a few examples. First of all, we see what is the difference between standard interest and compound interest. For instance, with a 10% annual interest and a 1000 principal:
| Year | Standard | Compound |
| 0 | $1,000 | $1,000 |
| 1 | $1,100 | $1,100 |
| 2 | $1,200 | $1,210 |
| 3 | $1,300 | $1,331 |
| 4 | $1,400 | $1,464 |
| 5 | $1,500 | $1,611 |
| 6 | $1,600 | $1,772 |
| 7 | $1,700 | $1,949 |
| 8 | $1,800 | $2,144 |
| 9 | $1,900 | $2,358 |
| 10 | $2,000 | $2,594 |
As you can see, compound interest quickly becomes much more interesting than standard interest. This table shows what some people call the magic of compounding, in which small increments of the principal make a lot of difference. It takes ten years to double the sum with standard interest, while it only takes more than seven years for compound interest.
We can also compare the compounding frequencies. For instance, with a 10% yearly interest rate but compounding at different periods:
| Periods | After five years | After ten years |
| 1 | $16,105 | $25,937 |
| 2 | $16,289 | $26,533 |
| 3 | $16,353 | $26,743 |
| 4 | $16,386 | $26,851 |
| 6 | $16,419 | $26,960 |
| 12 | $16,453 | $27,070 |
| 365 | $16,486 | $27,179 |
As you can see, the more often the interest compounds, the better it gets. Getting interest payments twice at 5% per year instead of once at 10% can make a significant difference. Of course, you can generally not choose the compound perioding of your investments. But it is still interesting to know!
Compounding effects
Here is how that looks on a graph for more visual people. Here is the difference between 3% standard interest and 3% compound interest over 20 years:
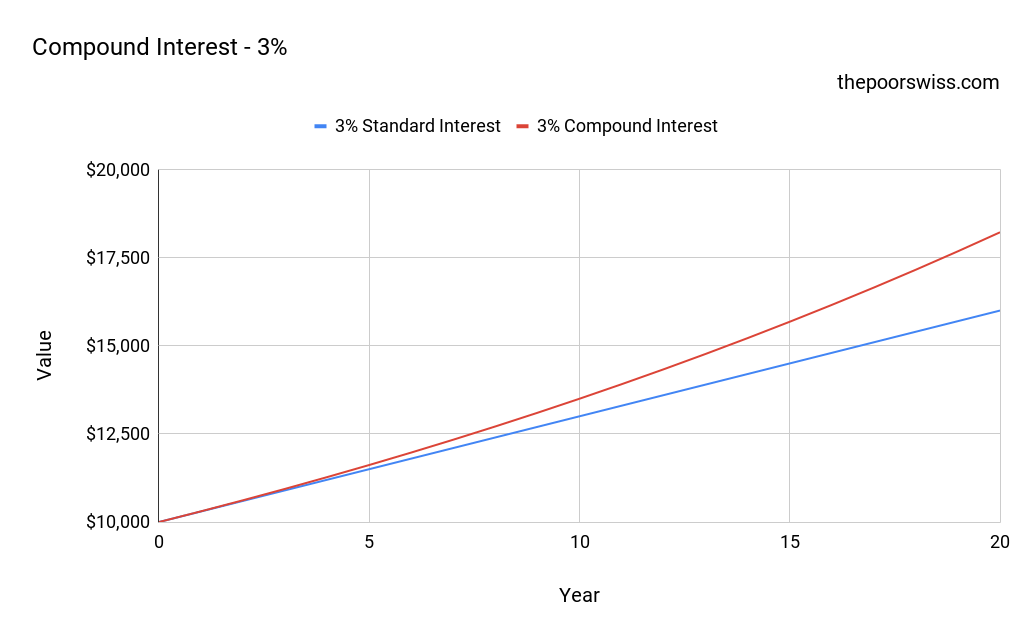
We can see that even with a small interest rate, the difference in compounding is quite essential. If we increase the interest rate to 8%:
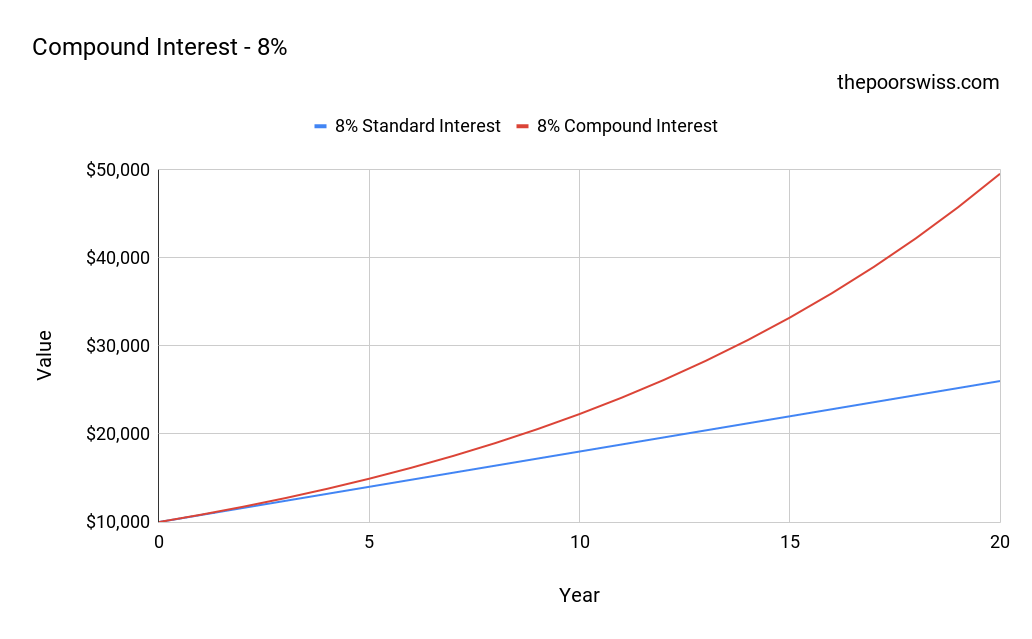
The difference is much more dramatic with a higher interest rate. This represents well what people are calling the magic of compounding!
Magic of compounding
The magic of compounding, as many people call it, happens over the long term. For instance, 10’000 dollars with 10% annual interest will grow to 174’494 dollars after 30 years. If you are saving for the long term, this is incredible.
And it gets even more incredible when you consider contributions to the account over the years. For example, if you add 200 dollars per month to the previous example, you will end up with 569’279 dollars after 30 years. And you will only have contributed 82’000 dollars. That is almost a gain of 500’000 dollars over 30 years. This is not bad.
Compound interest is highly related to starting to invest early. The earlier you start, the easier it will get to have significant returns with compounding. Compound interest is one of the reasons you should start investing early.
The rule of 72
You may have heard already of the rule of 72. It is a simple approximation that lets you estimate when the principal will have doubled its value based on the annual returns. The rule is relatively simple: divide 72 by the yearly returns, giving you the years to double your principal.
For instance, if you have 10% annual returns, it should double after 7.2 years. Of course, it is only an approximation, the real number being 7.27 years. But it is a reasonably good approximation. Here is the comparison between the rule of 72 and the Real answer, rounded, for some returns:
| Return | Rule of 72 | Real |
| 2% | 36 | 35.00 |
| 3% | 24 | 23.45 |
| 5% | 14.4 | 14.21 |
| 10% | 7.2 | 7.27 |
| 20% | 3.6 | 3.80 |
| 25% | 2.88 | 3.11 |
| 50% | 1.44 | 1.71 |
| 75% | 0.96 | 1.24 |
| 100% | 0.72 | 1.00 |
We can observe that the approximation is really good for small numbers. But it gets worse and worse as we have bigger returns. Some people prefer to use the rule of 69.3, which is sometimes a bit more precise for small numbers. But it is less convenient!
However, using this rule for investment returns is fine since we should not expect more than 10% annual returns. It is much easier than computing log(2)/log(1+return) in the head, right?
Compound interest in the stock market
Most people talk about the compounding effect of stock market returns. However, the stock market does not compound. A compound interest keeps the same interest all the time. The stock market is much more volatile. And there will be some days and months when your portfolio is down. And that is fine.
The primary difference comes with negative years. If your portfolio is down 10% a year and up 10% the next year, it is still down. This difference is because 10% of 90% of the original portfolio is only 9% and not 10%. It makes it difficult to talk about compounding effects in the stock market.
In the long term, the effects of the stock market can be described as compound interest. Indeed, if you use a realistic yearly rate of return over the long term, you can use compound interest and the Rule of 72 to describe your stock market returns. You need to be aware that this is not the same.
Compound interest is not always good
Sometimes compound interest can also play in your disfavor! Indeed, your bank account and stock market returns are not the only things that can compound. Your credit card debts compound in the same way.
Credit card balances have very high interest, often more than 10%. And it compounds daily. We saw before that the more frequently interest compounds, the stronger their effect. It is very real for credit card debt. Negative Compound Interest is how credit card companies make much money. For instance, if you have a credit card debt of 5000 dollars with a 12% annual interest rate, it will become 9’110 dollars after five years if you do not pay it!
The magic of compounding results can also play against you. You should never carry compounding debt with a high annual interest rate!
Another example is that currency inflation is also compounding. That means an inflation rate of 3% will also compound year after year. After ten years, it will not be 30%, but 34.4%. It makes inflation even harder to fight since it compounds!
FAQ
What is compound interest?
Compound interest is a way of computing interests based not only on the principal but also on previously earned interests.
Why is compound interest so great?
Compound Interest increases your money much faster than standard interest. Compound interest makes investing much more interesting.
What is the Rule of 72?
The Rule of 72 states that if you divide 72 by the interest rate of an instrument, you will know in how many years your principal will double. For instance, returns of 8% per year will double your investment every nine years. This rule is only a rule of thumb since it is an estimation, not the real number of years.
Conclusion
Compound interest is a powerful tool that will help you achieve Financial Independence.
It is not magic. It is just math. But there is no denying that its effects are very powerful. It will make your money grow faster than with standard interest. And it is essential to know how this works in practice. Because of how it works, it is necessary to start investing early!
If something is compounding, you can use the Rule of 72 to estimate when the value will double. We can apply compound interest to the stock market in the long term even though it does not compound like a bank account would. Finally, even though compound interest is great, it can also play against you! Your credit card debt will also compound!
What do you think about compound interest?
Download this e-book and optimize your finances and save money by using the best financial services available in Switzerland!
Download The FREE e-bookRecommended reading
- More articles about Investing Fundamentals
- More articles about Investing
- Who is Warren Buffett ? The Man and His Investments
- How to Choose an Index ETF Portfolio?
- Investing Fees could cost you your early retirement!

How can I do compound intetest with degiro?
I am not sure I understand your question. On the stock market, you compound by holding your stocks for a long time, and each return compound over the previous ones. This is the same with every broker.
It’s not magic but it work almost like a miracle! Nice and great post, keep it up!!
Hi Wolves,
You are absolutely right! It’s pretty simple math, but the effects are greater than we might think.
Thanks for stopping by!
I totally agree with your post “Compound interest is not magic it is only math” they’ve been mistakenly identifying it as a magic because of what it does. By the way thanks for this great post. Looking forward for you in posting more articles like this.
Hi Millionaire Mob,
You’re welcome! I am glad you like the post.
There is no denying that compound interest is great. But it’s simple math and by saying it’s magic, people will often think it’s complex but it’s a very simple formula.
I hope you will like future posts as well!
Thanks for sharing!
Hi Mr. The Poor Swiss.
Great post. Many people do not understand it or even do not give it attention, especially when we have small yearly interests as we have in Europe. As an investor seeking passive income generated from dividends, I really pay attention to it and appreciate how the companies that I invest compound the dividends over years.
All the best and success on your journey.
Cheers!
Hi Odysseus,
Yes, as you said, many people do not really understand it.
European interests are pretty bad these days. Dividends are a really good example of compounding indeed :) Passive income can compounds as well.
All the best on your journey too!
Thanks for stopping by.
Unfortunately inflation is also compounding. An that is rarely mentioned. That is why 100$ now is very far from what it was worth 20 years ago :-( Not to mention £ in the lats decade or so.
That’s a very good point Zoli. I didn’t think about the example of inflation. It’s probably the best example of where compound interest plays against us. I will add it to the article!
Thanks for stopping by!
Compound interest might not be magic, its effects sure are magical! When you know this, you know to start early. Thanks for these nice examples!
As you said, it only shows how important it is to start early!
Thanks for stopping by B!
Compound interest is a very powerful ally for everybody’s retirement planning, I totally agree. unfortunately it’s underestimated by the average person in magnitudes, so most people start saving (too) late. Have you seen my recent blogpost on this? https://www.smolio.ch/de/wissen/detail/zinseszins-effekt-dein-verbuendeter-fuer-die-altersvorsorge Cheers Thomas
Hi Thomas,
Yes, you’re right that’s underestimated. Everybody seems to start to save money very late in the game.
I haven’t seen your blog post no. My German is too bad to enjoy reading articles.
Thanks for stopping by!