Qu’est-ce que l’intérêt composé ? Est-ce de la magie ?
| Mis à jour: |(Information: certains des liens ci-dessous peuvent être des liens d'affiliation)
Les intérêts composés sont un sujet que vous pouvez lire sur la plupart des blogs consacrés aux finances personnelles. J’en ai déjà parlé un peu. Mais je ne me suis jamais plongé dedans. Il est maintenant temps de couvrir les intérêts composés en détail.
Beaucoup de gens vous diront que les intérêts composés sont comme de la magie ! Toutefois, il ne s’agit que de mathématiques. Mais comment calculer les intérêts composés ? Même s’il ne s’agit pas de magie, ses effets sont plus puissants qu’il n’y paraît à première vue. Les résultats de la capitalisation rendent l’investissement dans le marché boursier si attrayant. Mais le marché boursier est-il composé ? Nous allons tenter de répondre à ces questions dans cet article.
Je pense que beaucoup de gens ne comprennent pas correctement que les intérêts composés. Cet article vous aidera à comprendre l’intérêt composé et pourquoi il est excellent.
Intérêt composé
Nous commencerons par une citation attribuée à Albert Einstein :
Les intérêts composés sont la plus grande découverte mathématique de tous les temps.
Il y a une certaine controverse quant à savoir s’il a dit cela. Les gens lui attribuent plusieurs citations sur les intérêts composés, comme le fait de dire que c’est la huitième merveille du monde ou même de dire que c’est la force la plus puissante de l’univers. Au fil des ans, de nombreuses citations ont été attribuées à tort à Einstein. Je ne serais pas surpris qu’il n’ait rien dit de tel.
Peu importe qui a dit quoi, l ‘intérêt composé est un instrument puissant.
Les intérêts composés sont simples à comprendre. Les intérêts composés sont des intérêts sur des intérêts. L’intérêt standard ne rémunère que le capital. Cependant, avec les intérêts composés, le principal comprend tous les intérêts précédents que vous avez reçus. Cela signifie que vous percevez des intérêts sur un capital de plus en plus important. La différence peut sembler minime, mais elle est importante. L’intérêt composé rapportera toujours plus que l’intérêt normal.
Mais ce n’est pas de la magie. L’intérêt composé est un calcul simple, comme nous le verrons dans la section suivante. Et presque tout est composé de nos jours. Même si les résultats sont excellents, je n’appellerais pas cela de la magie.
Calcul de la valeur future
Maintenant, nous allons devoir faire quelques calculs. Étant donné que les intérêts sont calculés sur le capital accumulé et pas seulement sur le capital de base, il est un peu plus compliqué de calculer la valeur future de votre argent qu’avec les intérêts standard, où c’est trivial.
Tout d’abord, il est nécessaire de connaître les intérêts (I) et le principal (P), bien sûr. Mais vous devez également connaître la période de capitalisation. Il s’agit de la fréquence de la capitalisation ou du moment où les intérêts sont calculés. Pour la plupart des banques, la capitalisation se fait quotidiennement. Pour calculer les intérêts composés sur le marché boursier, il faut prendre en compte les rendements annuels moyens en tant qu’intérêts et une période annuelle.
Une fois que vous avez toutes ces valeurs, vous pouvez calculer la valeur future (VF) de votre argent après n périodes de capitalisation avec cette formule :
FV = P ( 1 + I ) ^ n
Cette formule ne fonctionne que si l’intérêt (I) est dans la même unité de temps que n. En général, vous avez un taux d’intérêt annuel (r) et quelques périodes de composition par an (t) :
FV = P ( 1 + r/n ) ^ nt
Ces formules vous donneront la valeur de votre argent dans le futur.
Bien entendu, vous n’êtes pas obligé de faire les calculs vous-même si vous ne le souhaitez pas. En effet, il existe sur Internet de nombreuses calculatrices qui feront parfaitement l’affaire pour vous. Par exemple, la calculatrice du site investor.gov est assez bonne. Elle est gérée par la Commission américaine des valeurs mobilières et des changes (SEC), qui réglemente de manière intéressante le marché boursier. La calculatrice de financial-calculators.com est également assez facile à utiliser et dispose de plus d’options. Et il existe des centaines d’autres calculatrices sur l’internet si vous n’êtes pas satisfait de ces deux-là.
Quelques exemples
Nous pouvons voir le résultat à l’aide de quelques exemples. Tout d’abord, nous verrons quelle est la différence entre l’intérêt standard et l’intérêt composé. Par exemple, avec un intérêt annuel de 10% et un capital de 1000 :
| Année | Standard | Composé |
| 0 | $1,000 | $1,000 |
| 1 | $1,100 | $1,100 |
| 2 | $1,200 | $1,210 |
| 3 | $1,300 | $1,331 |
| 4 | $1,400 | $1,464 |
| 5 | $1,500 | $1,611 |
| 6 | $1,600 | $1,772 |
| 7 | $1,700 | $1,949 |
| 8 | $1,800 | $2,144 |
| 9 | $1,900 | $2,358 |
| 10 | $2,000 | $2,594 |
Comme vous pouvez le constater, l’intérêt composé devient rapidement beaucoup plus intéressant que l’intérêt standard. Ce tableau illustre ce que certains appellent la magie de la capitalisation, dans laquelle de petites augmentations du capital font une grande différence. Il faut dix ans pour doubler la somme avec l’intérêt standard, alors qu’il ne faut que plus de sept ans pour l’intérêt composé.
Nous pouvons également comparer les fréquences de capitalisation. Par exemple, avec un taux d’intérêt annuel de 10 % mais composé à des périodes différentes :
| Périodes | Après cinq ans | Après dix ans |
| 1 | $16,105 | $25,937 |
| 2 | $16,289 | $26,533 |
| 3 | $16,353 | $26,743 |
| 4 | $16,386 | $26,851 |
| 6 | $16,419 | $26,960 |
| 12 | $16,453 | $27,070 |
| 365 | $16,486 | $27,179 |
Comme vous pouvez le constater, plus les intérêts sont composés, plus ils sont intéressants. Le fait de recevoir deux fois des paiements d’intérêts à 5% par an au lieu d’une fois à 10% peut faire une différence significative. Bien entendu, vous ne pouvez généralement pas choisir la période de composition de vos investissements. Mais c’est quand même intéressant à savoir !
Effets combinés
Pour les plus visuels, voici ce que cela donne sur un graphique. Voici la différence entre un intérêt normal de 3 % et un intérêt composé de 3 % sur 20 ans :
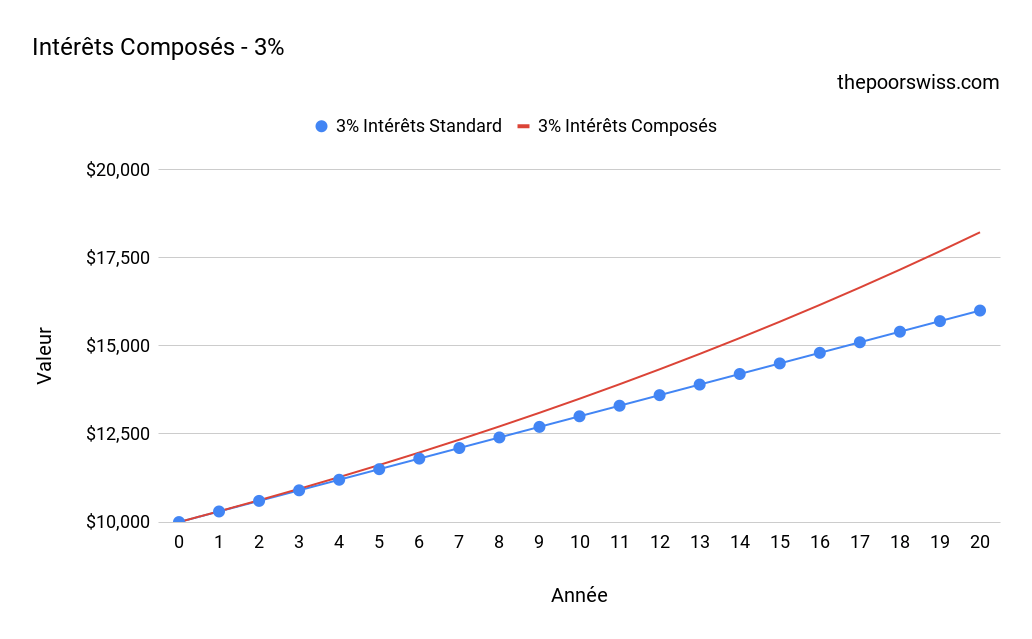
Nous pouvons constater que même avec un taux d’intérêt faible, la différence de capitalisation est tout à fait essentielle. Si nous augmentons le taux d’intérêt à 8% :
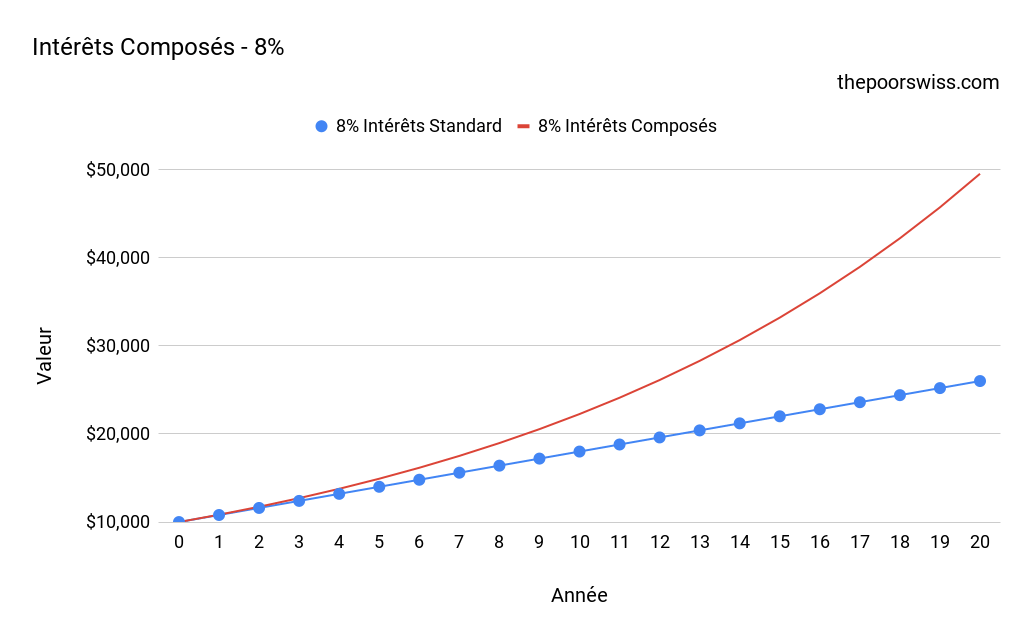
La différence est beaucoup plus importante avec un taux d’intérêt plus élevé. Cela représente bien ce que les gens appellent la magie de la capitalisation!
La magie de la composition
La magie de la capitalisation, comme beaucoup l’appellent, s’opère sur le long terme. Par exemple, 10’000 dollars avec un intérêt annuel de 10% atteindront 174’494 dollars après 30 ans. Si vous épargnez pour le long terme, c’est incroyable.
Et c’est encore plus incroyable si l’on considère les contributions au compte au fil des ans. Par exemple, si vous ajoutez 200 dollars par mois à l’exemple précédent, vous vous retrouverez avec 569’279 dollars après 30 ans. Et vous n’aurez contribué qu’à hauteur de 82’000 dollars. Cela représente presque un gain de 500 000 dollars sur 30 ans. Ce n’est pas mauvais.
L’intérêt composé est fortement lié au fait de commencer à investir tôt. Plus vous commencez tôt, plus il vous sera facile d’obtenir des rendements importants grâce à la capitalisation. Les intérêts composés sont l’une des raisons pour lesquelles vous devriez commencer à investir tôt.
La règle des 72
Vous avez peut-être déjà entendu parler de la règle du 72. Il s’agit d’une simple approximation qui vous permet d’estimer à quel moment le capital aura doublé sa valeur sur la base des rendements annuels. La règle est relativement simple : divisez 72 par les rendements annuels, ce qui vous donne le nombre d’années nécessaires pour doubler votre capital.
Par exemple, si vous avez un rendement annuel de 10 %, il devrait doubler après 7,2 ans. Bien entendu, il ne s’agit que d’une approximation, le chiffre réel étant de 7,27 ans. Mais c’est une approximation raisonnablement bonne. Voici la comparaison entre la règle de 72 et la réponse réelle, arrondie, pour certains retours :
| Retourner à | Règle de 72 | Real |
| 2% | 36 | 35.00 |
| 3% | 24 | 23.45 |
| 5% | 14.4 | 14.21 |
| 10% | 7.2 | 7.27 |
| 20% | 3.6 | 3.80 |
| 25% | 2.88 | 3.11 |
| 50% | 1.44 | 1.71 |
| 75% | 0.96 | 1.24 |
| 100% | 0.72 | 1.00 |
Nous pouvons observer que l’approximation est vraiment bonne pour les petits nombres. Mais c’est de pire en pire au fur et à mesure que nous avons des retours plus importants. Certaines personnes préfèrent utiliser la règle de 69,3, qui est parfois un peu plus précise pour les petits nombres. Mais c’est moins pratique !
Toutefois, l’utilisation de cette règle pour les rendements des investissements est acceptable, puisque nous ne devons pas espérer plus de 10 % de rendement annuel. C’est beaucoup plus facile que de calculer log(2)/log(1+retour) dans la tête, non ?
Les intérêts composés en bourse
La plupart des gens parlent de l’effet composé des rendements boursiers. Cependant, le marché boursier n’est pas composé. Un intérêt composé conserve le même intérêt tout le temps. Le marché boursier est beaucoup plus volatile. Et il y aura des jours et des mois où votre portefeuille sera en baisse. Et c’est bien.
La principale différence concerne les années négatives. Si votre portefeuille est en baisse de 10 % une année et en hausse de 10 % l’année suivante, il est toujours en baisse. Cette différence s’explique par le fait que 10% de 90% du portefeuille initial ne représentent que 9% et non 10%. Il est donc difficile de parler des effets composés sur le marché boursier.
À long terme, les effets du marché boursier peuvent être décrits comme des intérêts composés. En effet, si vous utilisez un taux de rendement annuel réaliste sur le long terme, vous pouvez utiliser l’intérêt composé et la règle de 72 pour décrire vos rendements boursiers. Vous devez savoir que ce n’est pas la même chose.
Les intérêts composés ne sont pas toujours bons
Parfois, les intérêts composés peuvent aussi jouer en votre défaveur ! En effet, votre compte bancaire et les rendements boursiers ne sont pas les seules choses qui peuvent être composées. Vos dettes de carte de crédit s’accumulent de la même manière.
Les soldes des cartes de crédit sont assortis d’intérêts très élevés, souvent supérieurs à 10 %. Et cela s’aggrave chaque jour. Nous avons vu précédemment que plus les composés d’intérêt sont fréquents, plus leur effet est important. C’est très réel pour les dettes de cartes de crédit. C’est grâce aux intérêts composés négatifs que les sociétés de cartes de crédit gagnent beaucoup d’argent. Par exemple, si vous avez une dette de carte de crédit de 5000 dollars avec un taux d’intérêt annuel de 12%, elle deviendra 9’110 dollars après cinq ans si vous ne la payez pas !
La magie de la composition des résultats peut également jouer contre vous. Il ne faut jamais avoir de dettes composées avec un taux d’intérêt annuel élevé!
Un autre exemple est que l’inflation monétaire est également composée. Cela signifie qu’un taux d’inflation de 3 % sera également composé année après année. Après dix ans, il ne sera plus de 30%, mais de 34,4%. Cela rend l’inflation encore plus difficile à combattre puisqu’elle s’aggrave !
FAQ
Qu’est-ce que l’intérêt composé ?
Les intérêts composés sont une façon de calculer les intérêts en se basant non seulement sur le capital mais aussi sur les intérêts précédemment acquis.
Pourquoi les intérêts composés sont-ils si importants ?
Les intérêts composés augmentent votre argent beaucoup plus rapidement que les intérêts normaux. Les intérêts composés rendent les investissements beaucoup plus intéressants.
Qu’est-ce que la règle de 72 ?
La règle de 72 stipule que si vous divisez 72 par le taux d’intérêt d’un instrument, vous saurez en combien d’années votre capital aura doublé. Par exemple, un rendement de 8 % par an permet de doubler votre investissement tous les neuf ans. Cette règle n’est qu’une règle empirique puisqu’il s’agit d’une estimation et non du nombre réel d’années.
Conclusion
Les intérêts composés sont un outil puissant qui vous aidera à atteindre l’indépendance financière.
Il est pas de la magie. C’est juste des maths. Mais il est indéniable que ses effets sont très puissants. Il fera fructifier votre argent plus rapidement qu’avec un intérêt standard. Et il est essentiel de savoir comment cela fonctionne dans la pratique. En raison de son fonctionnement, il est nécessaire de commencer à investir tôt!
Si quelque chose est composé, vous pouvez utiliser la règle de 72 pour estimer quand la valeur doublera. Nous pouvons appliquer l’intérêt composé au marché boursier à long terme, même s’il n’est pas composé comme le serait un compte bancaire. Enfin, même si les intérêts composés sont formidables, ils peuvent aussi jouer contre vous ! Votre dette de carte de crédit va également s’accroître!
Que pensez-vous des intérêts composés ?
Téléchargez cet e-book et optimisez vos finances et économisez de l'argent en utilisant les meilleurs services financiers disponibles en Suisse!
Télécharger l'e-book GRATUIT