What is the Modern Portfolio Theory?

Modern Portfolio Theory

The Modern Portfolio Theory was created in 1952 by Harry Markowitz. The author of the theory received the Nobel Prize in Economics in 1990 for this theory.

This theory is used by many asset managers to design portfolios. The theory defines a framework for choosing an asset allocation.

The primary motto of the theory is that for a given level of risk, there is an optimal portfolio. So, each investor can choose his level of risk, and from that, a portfolio with a specific asset allocation can be defined.

If you want to learn everything about the theory, you can read the original paper called Portfolio Selection. However, the original paper is very mathematical and quite complicated. Hopefully, my article will be more accessible than the original paper.

How does the theory work?

The goal of this theory is to devise a portfolio that will maximize returns for a given level of risk.

First, it is necessary to define the asset classes that will be considered in the analysis. For instance, we could consider the following asset classes:

• Small-Cap Stocks
• Large-Cap Stocks
• Long-Term Government Bonds

Then, for each of these asset classes, you will need three pieces of information:

• The Average Return of the asset class
• The standard deviation of the returns
• The correlation with each of the other asset classes

I realized an example with historical data for three U.S. Asset classes:

Then, you can start evaluating portfolios for these three asset classes. You will generate many possible allocations that will represent your portfolio.

And for each of these portfolios, you will have to compute two things:

• The average returns of the portfolio
• The volatility of the portfolio

You can find the formulas and the math for these two in the original paper.

Once you have these two numbers, you can make a graph with the volatility on the horizontal axis and the returns on the vertical axis. In my case, this gives me this graph:

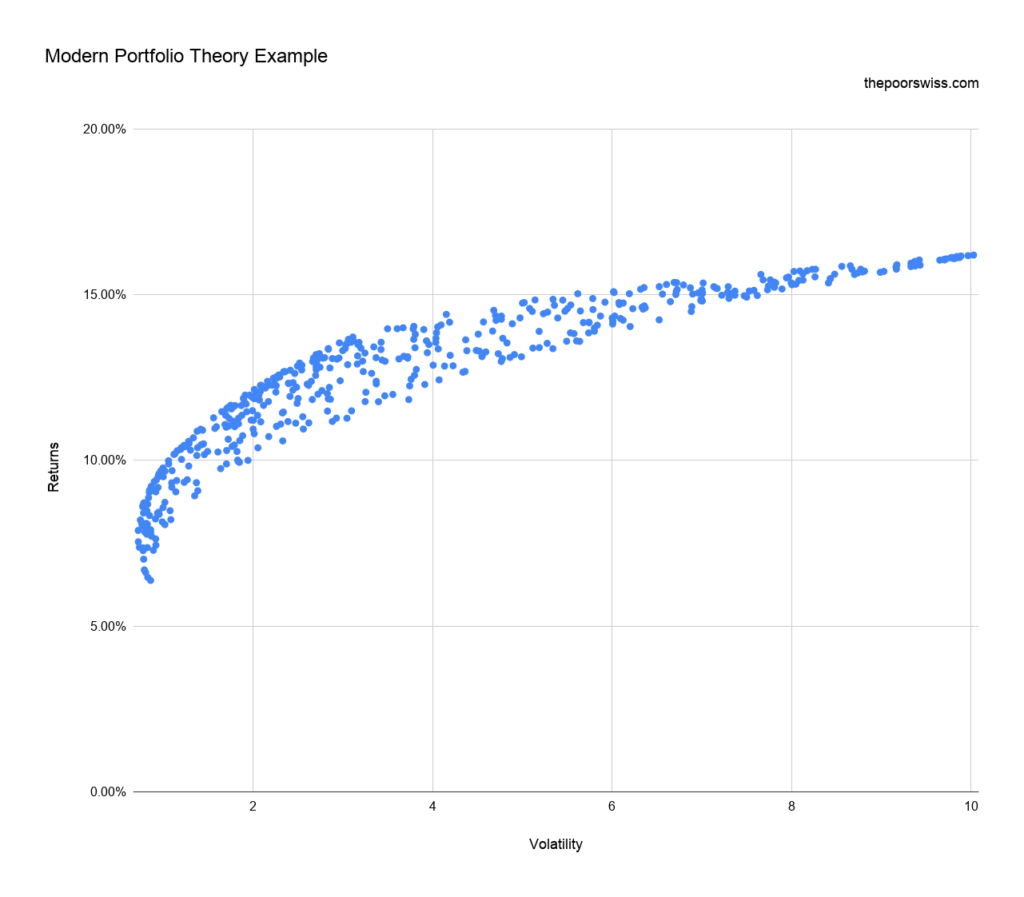
The Efficient Frontier

Now, for a given return, people are only interested in the portfolio with the lowest volatility. So, you are only interested in the portfolios on the left side of each row. The line of the interesting portfolio is called the Efficient Frontier.

Here is the same graph with the Efficient Frontier drawn (forgive my drawing!):

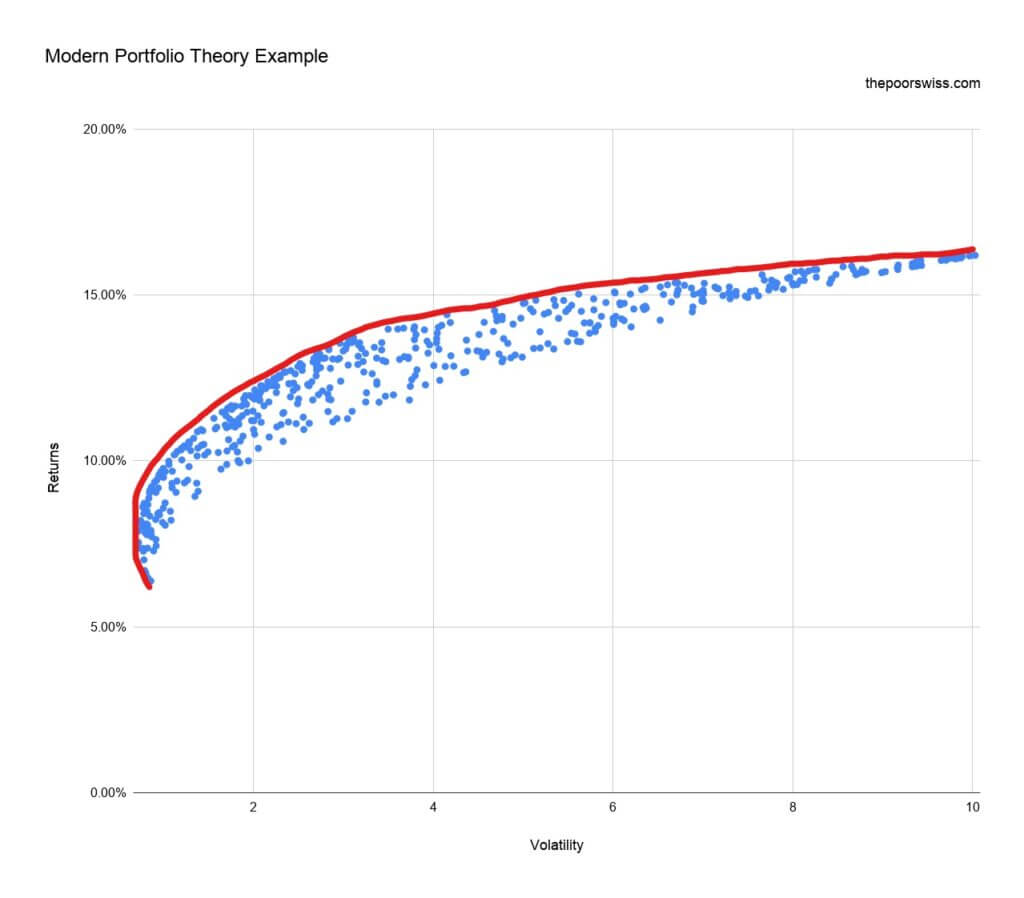
So, you must pick a portfolio on this line with a given amount of risk. It is interesting in this example that you can get very low volatility for about 10% of returns. But if you want 15% of returns, you will triple your volatility.

With this theory, there is an optimal portfolio for each given amount of risk.

Issues with the theory

Since its inception in the 1950s, there have been some people that have found issues with the theory.

One of the main issues with the theory is that it focuses on variance. The theory focuses on minimizing the variance. But in practice, people do not care about variance. People care about maximum drawdown. For instance, people are not bothered when one of their shares goes up by 30%, even though this has a significant variance. On the other hand, people care a lot when their portfolio goes down by 30%. People want to minimize drawdown, not variance.

Another issue with the theory is that it assumes that returns are independent from one year to another.  In practice, this assumption is not true. Markets often have a trend in one direction.

Another obvious issue is that the entire model rests on predicted values for the stock market. And there is no way to very accurately predict them in the long term. So, people mostly use historical data to get these values and decide on the portfolio. And sometimes, they change these values for the guessed future. But all the decisions rest on variables currently unknown.

The MPT will find the optimal portfolio for the amount of risk the client wants. And the asset classes are generally chosen by the client. But the problem with this choice is that investors are heavily biased. So the optimal portfolio is heavily tied to what the customer wants, not necessarily the customer’s needs.

Finally, in practice, exceptional (non-average) events happen much more often than the theory assumes. It is not uncommon to get higher-than-average returns or higher-than-average losses. These events do not fit well within the Modern Portfolio Theory.

Alternatives to the MPT

Since there are drawbacks to the Modern Portfolio Theory, there must be some alternatives.

The simplest alternative is simply to ignore this theory and to keep it simple, as we did on this blog. But it is not a real alternative to the MPT.

On the other hand, the Post Modern Portfolio Theory (PMPT) is a direct alternative to the MPT. It is an evolution of the MPT. Instead of using the variance of returns as risk, the PMPT uses the downside risk. The downside risk is how much an investor stands to lose. The downside risk represents a worst-case scenario for a given asset class.

The PMPT fixes the issue that investors do not care about the variance of higher returns, only the variance of low returns.

Another alternative is the theory of Behavioral Finance. These theories delve into investors’ minds. The idea is to consider that investors make errors and are influenced by their emotions, not facts.

These theories take into account many of the biases of the investors. For instance, investors generally prefer avoiding a loss to making a profit. All these biases are not taken into account by the MPT.

Unfortunately, there is no single Behavioral Finance theory. It is an entire field of financial analysis.

Conclusion

The Modern Portfolio Theory is interesting. It allows any customer to find an optimal portfolio for their risk.

On paper, it sounds great. You choose your asset classes, you give some inputs to the formulas, and you will find your optimal portfolio.

However, there are issues with this theory. First, it is complicated to get accurate values for the inputs of the theory. You will need to predict the returns and volatility of each of the asset classes. It is well-known that the market is unpredictable. So, we have to rely on historical data. And historical data is only a poor estimation of future results.

Also, I think it is too complicated. This theory tries to be too smart for me. I prefer to keep things very simple. I believe it is better to reduce the number of asset classes, maximize diversification, and keep things simple.

If you do not know where to start, you can read my article on how to design a stock market portfolio from scratch.

If you are interested in theories about the stock market, you will also be interested in the Efficient Market Hypothesis (EMH).

What do you think of the Modern Portfolio Theory?

Recommended reading

• More articles about Investing Fundamentals
• More articles about Investing
• How to start investing in the stock market in 2024?
• How to file your taxes with Swiss and foreign securities in 2024
• Index Replication in Details – ETFs and Mutual Funds